Probabilistic programming in about 100 lines of Julia
In my last post I speculated on the usefulness of probabilistic programming in geographic information systems (GIS). While I have played with some probabilistic programming languages (PPLs) like Turing, I mostly do statistical inference using my own code, specialized for the particular models I am trying to build. I wanted to learn more about how PPLs work to start thinking harder about how one might build a GIS around one. It turns out that it is not that hard to get a very rudimentary PPL up and running, so I thought I would share how I did that in (more or less) 100 lines of Julia code.
Getting started
using Distributions, LinearAlgebra, Statistics, CairoMakie, Random
Random.seed!(54332187)
The one dependency for our PPL is the Distributions package, which provides a standard interface for working with probability distributions. This is not strictly necessary, but it makes our lives a little easier. Otherwise we would have to write routines for sampling from and computing probability densities for every basic distribution that we want to use in our models. The LinearAlgebra and Statistics standard library modules just provide some functions that will be useful for analyzing our results, and CairoMakie is there to make plots, but none of those are crucial for the PPL implementation. You really can do this entirely in bare Julia.
Wrapping distributions with continuations
A strategy for implementing a really simple PPL is write the program in continuation-passing style (CPS) 1. We augment each probability distribution with a function that has a single argument, the result of sampling from the probability distribution, and returns another distribution, the next distribution in our probabilistic program. If this is a little confusing, it makes more sense in code. First we define a new type for our CPS distributions:
struct LatentDistribution f s d end
where f is the continuation function, s will be a symbol that we use to name each random variable, and d is the Distribution of the random variable.
The simple probabilistic model \(X \sim \mathcal{N}(0,1)\) now gets written using our LatentDistribution
model = LatentDistribution(X->nothing,:X,Normal(0,1))
Because we only have one variable in our probabilistic model, the continuation function takes the random variable X and outputs nothing, which we will use as a sentinel value to denote the end of our probabilistic program. When you have to write increasingly complex continations, Julia provides a convenient syntax for passing anonymous functions as the first argument to other functions, the do notation:
model = LatentDistribution(:X,Normal(0,1)) do X nothing end
This is identical to the previous model, but slightly easier to read. The benefits become even more clear when we consider a hierarchical model like
\begin{align} X &\sim \mathcal{N}(0,1) \\ Y | X &\sim \mathcal{N}(X,1). \end{align}This can be written as
model = LatentDistribution(:X,Normal(0,1)) do X LatentDistribution(:Y,Normal(X,1)) do Y # We don't need to explicitly return nothing end end
Continuation-passing style lets us create an environment in which downstream LatentDistributions know about earlier ones. The distribution for Y can use X as a parameter, because X is passed as an argument to the function that creates Y.
Sampling from the probabilistic program
The LatentDistribution objects that we have strung together with continuations don't do anything by themselves. They are, in a sense, a probabilistic program waiting to be run by an interpreter that we have yet to write. We can actually write many different interpreters, depending on the modeling task we want to accomplish. The most basic thing we want to do, however, is to draw random samples from the distribution defined by our probabilistic program.
For the two-level example, we need to do three things
- Sample
XfromNormal(0,1) - Construct the distribution of
Ygiven the just-sampled value ofX,Normal(X,1). - Sample
Yfrom that distribution
Sampling X is easy, the desired distribution is stored as the d field of model, so we can call X = rand(model.d). But how do we use this in our probabilistic program? Our continuations come to the rescue. Remember that model.f is the continuation that takes X as a parameter and returns the LatentDistribution for Y. So to sample Y, we would do rand(model.f(rand(model.d)).d), first constructing the LatentDistribution using the continuation and then sampling from the defined distribution.
Of course, in a more complicated probabilistic program, Y would itself be used to define other random variables, so you will want to call its continuation, and so on until you hit a variable whose continuation returns nothing. This calls for some recursion. We define a method
function draw(d::LatentDistribution) # Sample from the given distribution x = rand(d.d) # Call the continuation with the sampled value # and draw from that distribution draw(d.f(x)) end
We also need a method for when we hit nothing
draw(::Nothing) = nothing
We have a problem, though. If you run draw(model) using the model defined above, you will find that it returns nothing. We need to save the random variables that we have sampled. We can do this using a named tuple that associates the symbol of each LatentDistribution (model.s) with its sampled value.
function draw(d::LatentDistribution) # Sample from the given distribution x = rand(d.d) (;d.s => x, # Store the sampled value draw(d.f(x))...) # Recurse end draw(::Nothing) = (;) # Return an empty named tuple
And now, if we run draw(model), we get something like
(x = -0.2817850808916265, y = 0.6312531437930013)
Computing the probability
The next thing we'll need to do is to compute the (log) probability density for a given value sampled from the probabilistic program. For a basic d::Distribution, we do this with logpdf(d,x). For our probabilistic program, we recurse again, combining log probabilities by adding them:
function Distributions.logpdf(d::LatentDistribution,θ) # Extract the variable corresponding to the current # distribution x = θ[d.s] # Compute the logpdf of the current variable logpdf(d.d,x) + # Recurse logpdf(d.f(x),θ) end Distributions.logpdf(::Nothing,θ) = 0 # Start accumulating probability from 0
This is exactly the same structure as our draw function, except
- We call
logpdfrather thanrand. - We initialize the recursion with 0 rather than an empty named tuple.
- We combine the log probabilities by adding rather than concatenating.
Conditioning on observations
The final thing we want to do is statistical inference, estimating the latent variables given the values of observed random variables. We can do this with a new type representing observed variables
struct ObservedDistribution f s d y end
which is identical to LatentDistribution, except it has a field y that gives the value of the observation. We need to implement our sampling and log probability interpreters for ObservedDistribution
function draw(d::ObservedDistribution) y = d.y (;d.s=>y,draw(d.f(y))...) end function Distributions.logpdf(d::ObservedDistribution,θ) loglikelihood(d.d,d.y) + logpdf(d.f(d.y),θ) end
For sampling, we just return the observed value, while for log probability, we use the loglikelihood function from Distributions. This is just like the logpdf function, but computes the log probability for multiple independent and identically distributed observations, which is convenient.
Now we can write a model like
model = LatentDistribution(:X,Normal(0,1.0)) do X ObservedDistribution(:Y,Normal(X,1.0),[1.0;-0.2;0.3]) do Y end end
and sampling and log probability calculations will work.
Markov chain Monte Carlo sampling
There are many ways to approach inference in probabilistic programs, but we will focus on sampling from the posterior using Markov chain Monte Carlo sampling. Gibbs sampling samples each random variable in turn from its conditional distribution given all of the other distributions. This is only analytically possible for certain probability distributions, so we will instead sample from a different distribution, the proposal distribution, and then use rejection sampling to correct for the fact that the proposal is not necessarily the appropriate conditional distribution. This Metropolis-within-Gibbs sampling is fairly flexible, easy to implement, and lets us design efficient proposals for different parts of our model. The downside is that the proposal design is challenging to automate, so you'll need to do it by hand in our tiny PPL.
First, we will store our proposal distributions in a Dict from the symbols of each random variable to a function that takes a parameter value and returns a Distribution:
proposals = Dict(:X => θ -> Normal(θ.X,0.01))
This way the proposal distributions can depend on the current value of all of the sampled variables. For example, the true conditional probability distribution for our two-level normal model can be found analytically
proposals = Dict(:X => θ -> Normal(1/(1 + length(θ.Y)) * sum(θ.Y),inv(sqrt(1 + length(θ.Y)))))
Now our Gibbs sampling function will take a probabilistic program, the current value of the parameters, and the proposals Dict. For nothing and ObservedDistribution, we don't need to sample anything, so we just return the current parameters, and recurse if we need to.
gibbs(::Nothing,θ,proposals) = θ gibbs(d::ObservedDistribution,θ,proposals) = gibbs(d.f(d.y),θ,proposals)
For the LatentDistribution, we need to implement the Metropolis-Hastings transition kernel
function gibbs(d::LatentDistribution,θ,proposals) # Extract the current variable x = θ[d.s] # Construct the proposal distribution q = proposals[d.s](θ) # Sample from the proposal distribution x′ = rand(q) θ′ = (;θ...,d.s=>x′) # Construct the reversed proposal q′ = proposals[d.s](θ′) # Compute the log acceptance ratio α = logpdf(d,θ′) + logpdf(q′,x) - logpdf(d,θ) - logpdf(q,x′) # Rejection sampling if log(rand()) < α # Accept the proposal # and recurse return gibbs(d.f(x′),θ′,proposals) else # Reject the proposal # and recurse return gibbs(d.f(x),θ,proposals) end end
There is one trick here that works even though it is technically wrong. When we call logpdf(d,θ′) and logpdf(d,θ), we only compute the log probability for the variables of the model below the current variable in the chain of continuations. This is okay because the log probability of the other variables can't depend on the current variable. Otherwise we couldn't write the probabilistic program. Since only the current variable changes under the proposal, the log probability of the variables that don't depend on it is just a constant that cancels out in the acceptance ratio, so this works.
Example
As an example, we will fit the following Bayesian linear regression to some synthetic data
\begin{align} \beta &\sim \mathcal{N}(0,I) \\ \tau &\sim \Gamma(2,1) \\ Y | X,\beta,\tau &\sim \mathcal{N}(X\beta,\tau^{-1}) \end{align}# Generate some synthetic data N = 100 x = range(-1,1,length=N) X = [one.(x) x] β0 = [1.0;-1.0] σ0 = 1.0 Y = X * β0 .+ σ0 * randn(N) # Define the model model = LatentDistribution(:β,MvNormal(Diagonal(ones(2)))) do β LatentDistribution(:τ,Gamma(2,1)) do τ ObservedDistribution(:Y,MvNormal(X*β,inv(sqrt(τ))),Y) do Y end end end # Define the proposal distributions proposals = Dict(:β => θ -> MvNormalCanon(θ.τ*X'θ.Y,θ.τ*X'X+I), :τ => θ -> Gamma(2 + length(Y)/2,inv(1 + sum(abs2,θ.Y .- X*θ.β)/2))) # Draw an initial value from the model θ0 = draw(model) # Run 100000 Gibbs steps θs = accumulate((θ,i)->gibbs(model,θ,proposals),1:100000,init=θ0) βs = mapreduce(x->x.β,hcat,θs) τs = map(x->x.τ,θs) # Plot the results fig = Figure() ax1 = Axis(fig[1,1],xlabel="x",ylabel="Y") scatter!(ax1,x,Y) ax2 = Axis(fig[2,1],xlabel="β") density!(ax2,βs[1,:]) density!(ax2,βs[2,:]) vlines!(ax2,[β0[1]]) vlines!(ax2,[β0[2]]) ax3 = Axis(fig[3,1],xlabel="τ") density!(ax3,τs) vlines!(ax3,[inv(σ0^2)]) save("linear_regression.png",fig)
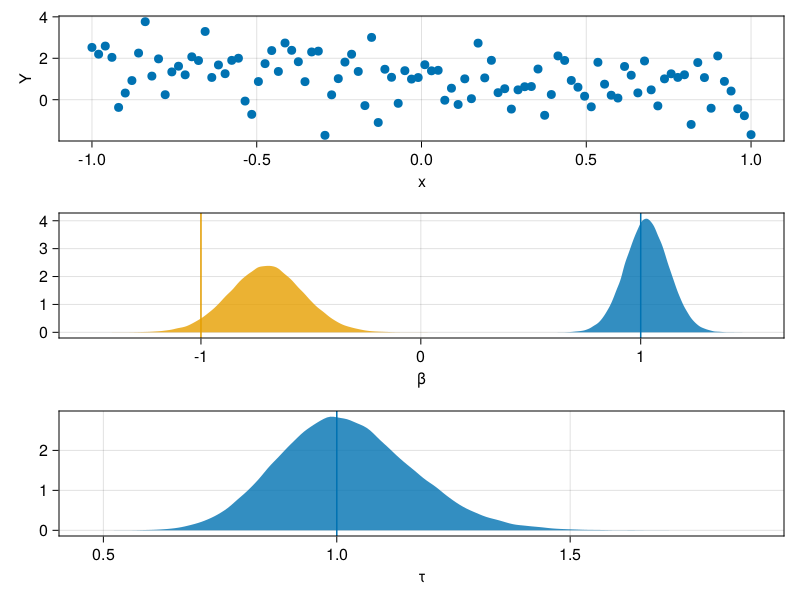
Conclusion
So there you have a rudimentary probabilistic programming language in only a few lines of Julia. Drawing random samples, computing log probabilities and Metropolis-within-Gibbs sampling from the posterior distribution are all just different interpreters of the same probabilistic program. We could conceivably implement other inference algorithms like Hamiltonian Monte Carlo or variational inference just by walking down the chain of continuations and accumulating the necessary information at each step.
There are many limitations to our tiny PPL. We have to write out the continuations explicitly in the do notation syntax. It doesn't support the stochastic control flow structures that distinguish true probabilistic programs from basic probabilistic models. It probably also doesn't perform very well with complicated models and big data.
I learned a lot from the following three references, which I highly recommend if you are interested in the inner workings of PPLs.
- Noah D. Goodman and Andreas Stuhlmüller. The Design and Implementation of Probabilistic Programming Languages. http://dippl.org/
- Jan-Willem van de Meent et al. An Introduction to Probabilistic Programming. https://arxiv.org/abs/1809.10756
- Jonathan Law and Darren Wilkinson. Functional probabilistic programming for scalable Bayesian modelling. https://arxiv.org/abs/1908.02062
Footnotes:
This idea comes from Goodman and Stuhlmueller's Design and Implementation of Probabilistic Programming Languages